Mise à jour du 21/01/2026
Si vous lisez ceci, c’est que vous vous intéressez à la rencontre improbable entre le patrimoine ancestral nord-africain et le code informatique.. Cet article, initialement publié en 2023, a été mis à jour pour raconter une histoire : celle d’une évolution. Vous y trouverez mes premières expérimentations… disons, « naïves », et, plus bas, mes recherches actuelles, beaucoup plus structurées. Bonne lecture !
Les origines et l’inspiration
Aujourd’hui, je suis ravi de partager avec vous mes curieuses explorations à l’intersection de l’art traditionnel et de la programmation. Mon projet vise à recréer les motifs captivants de la broderie et du tissage, en utilisant les outils de l’art génératif. Ce travail est un hommage à la richesse de la culture amazighe, où chaque tracé raconte une histoire, chaque géométrie révèle un sentiment.
Cet art séculaire incarne l’essence de la riche histoire et de la culture amazighe marocaine. Née d’une tradition ancestrale transmise de génération en génération, cette pratique est bien plus qu’un simple ornement : c’est un moyen de résistance, d’expression et de préservation de notre identité.
Caractérisée par ses compositions géométriques saisissantes, la broderie amazighe est un langage visuel. Elle raconte des légendes, exprime des croyances et reflète le quotidien. L’utilisation prédominante de formes comme les carrés, les triangles et les losanges, ainsi que leur agencement symétrique le long des axes X et Y (en répétition ou translation), n’est jamais un hasard esthétique. Cette logique géométrique représente l’équilibre, l’harmonie et reflète une profonde compréhension de la nature et de l’univers.
La « Période Pointilliste » (Mes débuts en 2023)
Au début de cette aventure, l’idée était de capturer cette essence en utilisant un algorithme conçu avec p5.js. À l’époque, mon approche était… disons, expérimentale (pour ne pas dire un peu brute de décoffrage !).
Mon premier algorithme dessinait des motifs dans une grille en utilisant des nuages de points. Je voyais cela comme une sorte de broderie numérique, point par point, pixel par pixel. L’algorithme plaçait des cercles de couleurs aléatoires de manière symétrique. Le résultat était une œuvre d’art dynamique, vibrante, un peu comme une explosion de confettis, mais qui manquait peut-être de la rigueur architecturale que je chéris tant aujourd’hui
Voici à quoi ressemblaient ces premières itérations :

Le fonctionnement était simple :
Phase 1 : On place aléatoirement entre 1 et 10 cercles, on leur donne 3 couleurs, et on les duplique en miroir.
Phase 2 : On ajoute une seconde couche de cercles (entre 4 et 24) pour densifier le tout.
Je le confessais moi-même à l’époque : « Je ne suis pas un développeur, mon code est brouillon ». Et c’était vrai ! Mais ce code avait le mérite d’explorer une question vertigineuse : le nombre de combinaisons possibles.
Même avec cette version simplifiée, le nombre de variations uniques dépassait l’entendement (plus de 114 sextillions de possibilités, rien que ça). C’était la preuve mathématique que la grammaire visuelle amazighe est infinie.
![]()
La somme s’étend de ![]() à
à ![]() , couvrant toutes les possibilités de 4 à 24 cercles dans un quart de motif. Cela tient compte de la symétrie du motif entier, où placer ( m ) cercles dans un quart de motif implique la présence de 4 fois ( m ) cercles dans l’ensemble du motif.
, couvrant toutes les possibilités de 4 à 24 cercles dans un quart de motif. Cela tient compte de la symétrie du motif entier, où placer ( m ) cercles dans un quart de motif implique la présence de 4 fois ( m ) cercles dans l’ensemble du motif.
Le retour aux fondamentaux (L’évolution 2026)
Depuis ce premier article, entre deux projets d’architecture (et quelques cafés), j’ai trouvé le temps d’explorer un peu plus cet univers, d’abord sous Grasshopper pour du prototypage rapide, puis en revenant à p5.js. Je pense avoir aujourd’hui assez affûté ma maîtrise du code créatif pour qu’il soit enfin à la hauteur de ma vision… du moins pour le moment !
Pourquoi ce retour ? Car au fond, il y avait un décalage frustrant dans mes premières expérimentations. Ma sensibilité marocaine et mon œil d’architecte ont toujours perçu le motif amazigh pour ce qu’il est réellement : une structure vectorielle, faite de tensions, de lignes nettes et de géométrie sacrée. Exactement comme nos fibules, nos tatouages ou les histoires racontées par les lignes d’un tapis.
En 2023, mes compétences techniques m’imposaient une limite. Le « nuage de points » de mes débuts était une abstraction forcée. Je dessinais par « taches » faute de savoir bâtir par « traits ».
Aujourd’hui, ce fossé est comblé. J’ai pu abandonner l’approximation des points pour revenir à l’essence du tracé : le vecteur, la ligne claire et la structure. J’ai donc décidé de tout reprendre à zéro. Exit les nuages de points colorés, place au noir et blanc, radical et précis.
Le passage à la géométrie vectorielle
J’ai développé un nouvel outil, beaucoup plus robuste. Au lieu de « jeter » des points sur une toile, ce nouveau système « tisse » des lignes. Il réfléchit comme un métier à tisser traditionnel (le fameux Azeṭṭa) : il y a une trame, une structure, et des règles de croisement strictes.
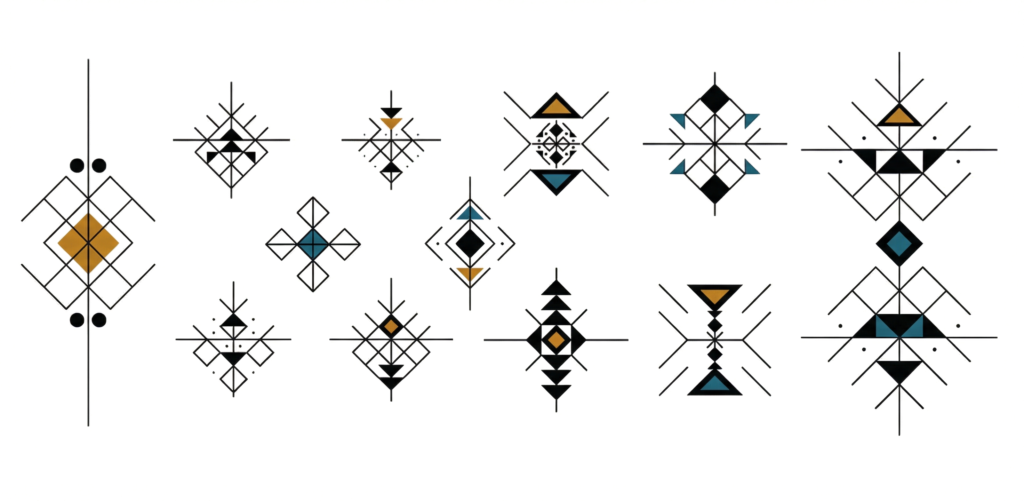
Voici quelques résultats issus de ce nouveau moteur de génération :
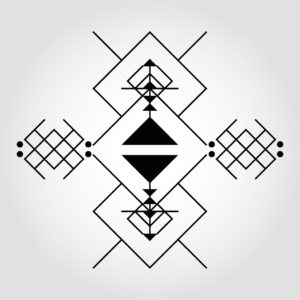

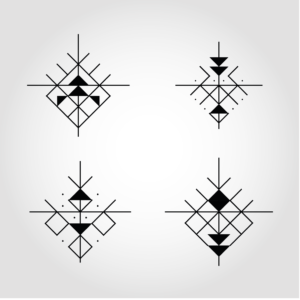
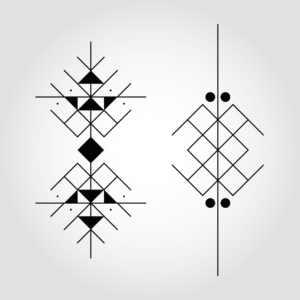
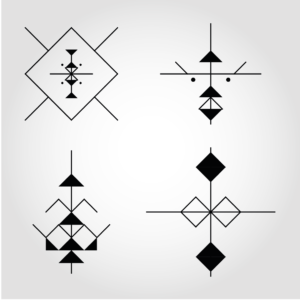
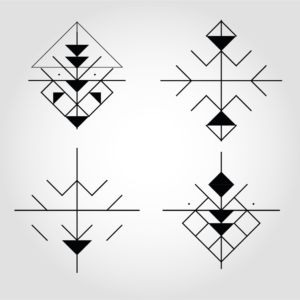

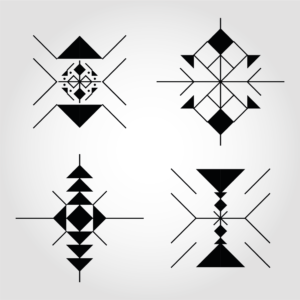
Vous voyez la différence ? On n’est plus dans l’illustration décorative, mais dans la construction.
- La pureté du trait : Les formes sont nettes, incisives, presque coupantes.
- La symbolique : On retrouve beaucoup mieux l’esprit des symboles protecteurs, des losanges (l’œil) et des zigzags (l’eau, le serpent).
- L’aspect « Maker » : Contrairement à la version colorée, ces nouveaux designs sont exploitables. On peut les envoyer vers un traceur (pen plotter), une découpeuse laser ou une imprimante 3D. Le virtuel devient physique.
Une logique simple pour une infinité de résultats
Ce qui me fascine avec cette nouvelle version, c’est qu’elle repose sur une logique géométrique finalement très simple, mais qui permet une complexité émergente folle.
Le programme ne « dessine » pas au hasard. Il construit des échafaudages invisibles, puis décide quelles lignes garder et quelles lignes effacer pour révéler le motif. C’est un dialogue constant entre le plein et le vide, exactement comme dans l’architecture.
Certains motifs générés ressemblent à des plans de cités futuristes, d’autres à des circuits imprimés, et pourtant, ils sont indéniablement ancrés dans notre patrimoine. C’est la preuve que cette esthétique est intemporelle : elle était moderne il y a 1000 ans, elle est futuriste aujourd’hui.
Je vous laisse découvrir quelques motifs amazigh générés avec cet algorithme, la suite juste après cette petite pause visuelle !







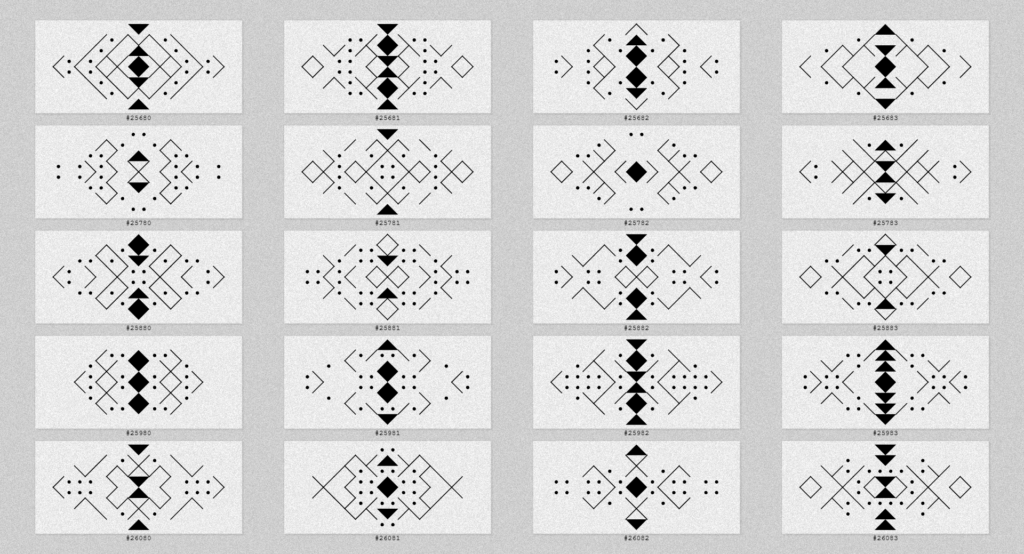
La suite ? … évidemment qu’il y aura une suite
Je travaille actuellement sur une suite encore plus ambitieuse de ce projet (je ne vous en dis pas plus pour l’instant, mais disons que ça va aller beaucoup plus loin dans l’interaction et la 3D… Stay tuned !).
En attendant, j’ai mis à jour mon « Laboratoire ». J’ai créé un outil en ligne qui utilise ce nouveau moteur de génération. Je vous invite à aller tester, à créer vos propres motifs, et à voir comment une logique simple peut créer une infinité de variations visuelle et symboliques
P.S. : Le code source de la première version est toujours disponible sur mon profil OpenProcessing pour les archéologues du numérique, mais je vous conseille vivement de jeter un œil aux nouvelles expérimentations.